티스토리 뷰
2장. 간단한 분류 알고리즘 훈련
길벗출판사의 머신러닝 교과서 실습입니다
수학적 배경
인공뉴런 : 두개의 클래스가 있는 이진분류 작업으로 볼 수 있다.
여기서 두개의 클래스를 -1, 1이라고 한다.
입력값
x와 벡터w의 선형 조합으로 결정함수phi(z)를 나타낸다.
선형 조합이란 구성하는 요소끼리 계수를 곱해서 더해서 나올수 있는 조합니다.
다르게 표 현하면 span이라고 볼수 있을것 같다.
최종입력 z는 x, z의 선형조합니다.
$$ z = w_1 x_1 + ... + x_m w_m $$
선형 조합을 각 집합 X, W의 행렬곱으로 표현할수 있다.
$ W = [ w_0 w_1 w_2 .. . w_m ] $는 가중치입니다.
x가 주어졌을때, 그 결과를 예측하기 위해서 단순히 x에다가 어떤 수를 곱한다고 합시다.
여기서 곱하는 값을 가중치라고 하며 주로 w로 나타냅니다.
지금은 x가 m개 존재하므로 가중치도 m개가 필요합니다.? 일단 지금은 그렇습니다.
회귀?
- 회귀 vs 분류?
- 선형회귀, 로지스틱회귀?
plt.scatter
plt.scatter( x축 , y축 , options )
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
plt.scatter([1.0, 2.0, 3.0 ,4.0, 5.0], #x축
[0.0, 0.9, 0.5, 0.5, 0.8], #y축
color='orange', marker='x', label='setosa')
plt.show()
코드를 이해해보자 으
$$ \eta = 에타 $$
파이썬 zip함수 : https://wikidocs.net/32#zip
판다스에서 csv파일 읽기pd.read_csv('04/iris.data', header=None)
퍼셉트론 분류기 클래스
매개변수
eta($ {\eta} $) | float | 학습률 (0.0과 1.0 사이)
n_iter | int | 훈련 데이터셋 반복 횟수
random_state | int | 가중치 무작위 초기화를 위한 난수 생성기 시드
속성
w_ : 1d-array : 학습된 가중치
errors_ : list : 에포크마다 누적된 분류 오류
메서드
__init__(self, eta=0.01, n_iter=50, random_state=1 ):
fit(self, X, y):
net_input(self, X):
predict(self, X):
import numpy as np
class Perceptron(object):
"""퍼셉트론 분류기
매개변수
------------
eta : float
학습률 (0.0과 1.0 사이)
n_iter : int
훈련 데이터셋 반복 횟수
random_state : int
가중치 무작위 초기화를 위한 난수 생성기 시드
속성
-----------
w_ : 1d-array
학습된 가중치
errors_ : list
에포크마다 누적된 분류 오류
"""
def __init__(self, eta=0.01, n_iter=50, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
"""훈련 데이터 학습
매개변수
----------
X : {array-like}, shape = [n_samples, n_features]
n_samples개의 샘플과 n_features개의 특성으로 이루어진 훈련 데이터
y : array-like, shape = [n_samples]
타깃값
반환값
-------
self : object
"""
# w_ 에 초기 값을 저장하는 list를 할당한다.
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1]) #요소가 3개짜리 리스트.
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
# x에 따른 y의 예측값을 self.predict(xi)로 구한다.
# y의 실제 값은 target이다.
# y의 실제값과 예측값을 비교한다.
# w_의 차이가 있으면 가중치를 업데이트한다..
for xi, target in zip(X, y):
#모든 x에 대하여 반복하는 것이 1에포크이다.(여기서 x는 2개 있으므로 2번 반복?)
#한번 할때마다 가중치값이 바뀐다.
#print("xi:", xi, " w_:", self.w_, " y:", target, "y_predict: ", self.predict(xi))
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0) #update가 0이 아니면 errors증가.
self.errors_.append(errors) # errors를 요소로 self.errors_에 추가한다.
return self
def net_input(self, X):
"""최종 입력 계산"""
# 입력 : [x x]모양, 출력은 스칼라값으로 나온다.
# 출력 : x값 곱하기 가중치, 그리고 절편(w_[0]) 을 더함.
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
"""Unit Step Function 를 사용하여 클래스 레이블을 반환합니다"""
# 입력 : [x x]모양
# 출력 : 0보다 크면 1, 작으면 -1 반환.
return np.where(self.net_input(X) >= 0.0, 1, -1)import pandas as pd
df = pd.read_csv('04/iris.data', header=None)
df.head()
#df.tail()
# print(df.head())
# 0 1 2 3 4
# 0 5.1 3.5 1.4 0.2 Iris-setosa
# 1 4.9 3.0 1.4 0.2 Iris-setosa
# 2 4.7 3.2 1.3 0.2 Iris-setosa
# 3 4.6 3.1 1.5 0.2 Iris-setosa
# 4 5.0 3.6 1.4 0.2 Iris-setosa
# print(df.tail())
# 0 1 2 3 4
# 145 6.7 3.0 5.2 2.3 Iris-virginica
# 146 6.3 2.5 5.0 1.9 Iris-virginica
# 147 6.5 3.0 5.2 2.0 Iris-virginica
# 148 6.2 3.4 5.4 2.3 Iris-virginica
# 149 5.9 3.0 5.1 1.8 Iris-virginica| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | Iris-setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | Iris-setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | Iris-setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | Iris-setosa |
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# setosa와 versicolor를 선택합니다
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1) #3항 연산자와 비슷함
# 꽃받침 길이와 꽃잎 길이를 추출합니다
# iloc[ ] 으로 df(위의 표) 에서 column의 값이 0,1인 데이터만 가져옴
X = df.iloc[0:100, [0, 2]].valuesprint("setosa의 꽃받침 길이와 꽃잎 길이")
print(" ", X[0, 0], X[1,0], "...", X[48,0], X[49,0])
print(" ", X[0, 1], X[1,1], "...", X[48,0], X[49,1])
print("y\n", y)
#print("X\n", X)setosa의 꽃받침 길이와 꽃잎 길이
5.1 4.9 ... 5.3 5.0
1.4 1.4 ... 5.3 1.4
y
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1]# 산점도를 그립니다
plt.scatter(X[:50, 0], X[:50, 1],
color='red', alpha=0.5, marker='o', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1],
color='blue', alpha=0.5, marker='x', label='versicolor')
plt.xlabel('sepal length [cm]',size=14)
plt.ylabel('petal length [cm]',size=14)
plt.legend(loc='upper left')
plt.show()
이제부터는 붓꽃 데이터 셋을 선형 분류기로 분류하려고 한다.
ppn = Perceptron(eta = 0.1, n_iter =10)
ppn.fit(X, y)
plt.plot(range(1,len(ppn.errors_)+1),ppn.errors_, marker='o')
plt.xlabel('Epochs',size=14)
plt.ylabel('Number of errors',size=14)
plt.show()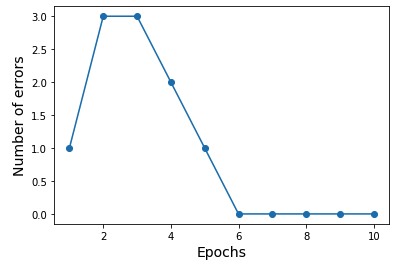
'Diary > Learned' 카테고리의 다른 글
| TIL 카테고리 추가 (0) | 2019.08.04 |
|---|---|
| TIL 2019-8-3 (0) | 2019.08.04 |
| TIL 2019-7-30 (0) | 2019.08.04 |
| 머신러닝 공부 일지(7/11 ~ 7/16) (0) | 2019.07.17 |
| 알고리즘 문제 풀이 check : DFS유형. (0) | 2019.04.13 |
